Математика – страница 77
На рисунке
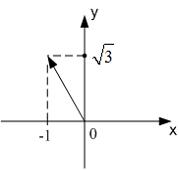
приведено геометрическое изображение комплексного числа. Его тригонометрическая форма записи имеет вид …

приведено геометрическое изображение комплексного числа. Его тригонометрическая форма записи имеет вид …
Из областей на комплексной плоскости, заданных соотношениями
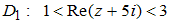 ;
;
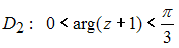 ;
;
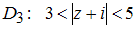 ;
;
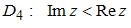 ,
,
односвязной не является область …
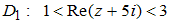 ;
;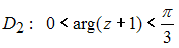 ;
;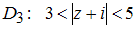 ;
;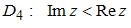 ,
,односвязной не является область …
Дано множество 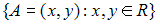 с метрикой
с метрикой 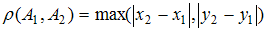 , где
, где 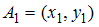 и
и 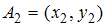 .
.
Тогда областью, соответствующей неравенству
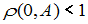 , где
, где 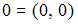 – начало координат, является …
– начало координат, является …
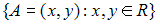 с метрикой
с метрикой 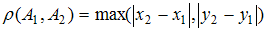 , где
, где 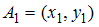 и
и 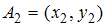 .
.Тогда областью, соответствующей неравенству
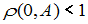 , где
, где 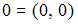 – начало координат, является …
– начало координат, является …Дана периодическая с периодом 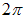 функция, которая для
функция, которая для 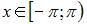 может быть записана в виде
может быть записана в виде
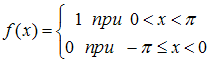 .
.
Если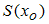 – значение суммы ряда Фурье для этой функции в точке
– значение суммы ряда Фурье для этой функции в точке 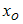 , то значение
, то значение 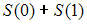 равно …
равно …
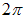 функция, которая для
функция, которая для 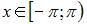 может быть записана в виде
может быть записана в виде 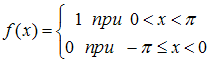 .
. Если
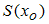 – значение суммы ряда Фурье для этой функции в точке
– значение суммы ряда Фурье для этой функции в точке 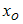 , то значение
, то значение 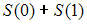 равно …
равно …Функция 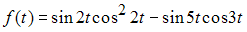 , представленная как сумма гармоник, имеет вид …
, представленная как сумма гармоник, имеет вид …
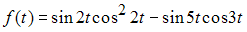 , представленная как сумма гармоник, имеет вид …
, представленная как сумма гармоник, имеет вид …Таблица
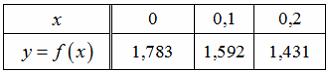
представляет значения функции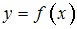 в некоторых точках.
в некоторых точках.
Используя формулы, основанные на интерполяционном полиноме Лагранжа, вычисляются, с тремя знаками после запятой, значения производной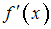 заданной функции в точках
заданной функции в точках 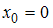 ,
, 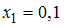 ,
, 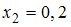 .
.
Тогда значения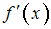 в указанных точках соответственно равны …
в указанных точках соответственно равны …

представляет значения функции
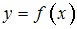 в некоторых точках.
в некоторых точках.Используя формулы, основанные на интерполяционном полиноме Лагранжа, вычисляются, с тремя знаками после запятой, значения производной
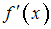 заданной функции в точках
заданной функции в точках 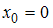 ,
, 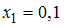 ,
, 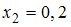 .
.Тогда значения
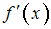 в указанных точках соответственно равны …
в указанных точках соответственно равны …Величины 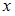 и
и 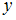 имеют предельные абсолютные погрешности
имеют предельные абсолютные погрешности 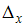 и
и 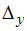 соответственно.
соответственно.
Тогда для предельных абсолютных погрешностей величин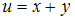 и
и 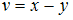 справедливо утверждение:
справедливо утверждение:
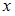 и
и 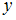 имеют предельные абсолютные погрешности
имеют предельные абсолютные погрешности 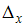 и
и 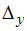 соответственно.
соответственно.Тогда для предельных абсолютных погрешностей величин
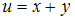 и
и 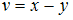 справедливо утверждение:
справедливо утверждение: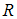 отображение
отображение 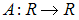 называется сжимающим, если…
называется сжимающим, если…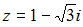 , то
, то 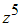 равно…
равно…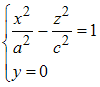 вокруг оси
вокруг оси 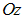 , имеет вид …
, имеет вид …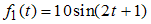 и
и 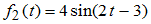 равна…
равна…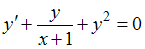 ,
, 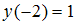 , имеет вид…
, имеет вид… и
и 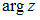 – модуль и главное значение аргумента комплексного числа
– модуль и главное значение аргумента комплексного числа 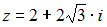 , то величина
, то величина 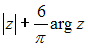 равна …
равна …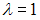 для уравнения
для уравнения 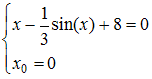 имеет вид…
имеет вид…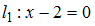 и
и 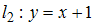 равен…
равен…