Математика – страница 35
В теории потребления предполагается, что функция полезности потребителя  не обладает свойством …
не обладает свойством …
 не обладает свойством …
не обладает свойством …Для определенного интеграла 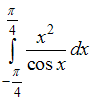 справедливо равенство …
справедливо равенство …
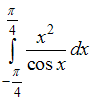 справедливо равенство …
справедливо равенство …Область определения функции  имеет вид …
имеет вид …
 имеет вид …
имеет вид …Матрица выигрышей в игре с природой имеет вид
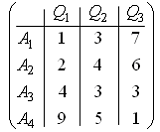
Тогда оптимальной по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем пессимизма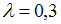 будет стратегия …
будет стратегия …

Тогда оптимальной по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем пессимизма
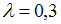 будет стратегия …
будет стратегия …Функция полезности потребителя имеет вид  , а оптимальное потребление:
, а оптимальное потребление:  ,
, 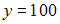 . Тогда предельная полезность блага
. Тогда предельная полезность блага 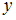 равна …
равна …
 , а оптимальное потребление:
, а оптимальное потребление:  ,
, 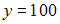 . Тогда предельная полезность блага
. Тогда предельная полезность блага 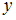 равна …
равна …Аксиомой линейного пространства  не является …
не является …
 не является …
не является …Значение определенного интеграла  принадлежит промежутку …
принадлежит промежутку …
 принадлежит промежутку …
принадлежит промежутку …Матрица выигрышей в игре с природой имеет вид:

Тогда средний выигрыш игрока по критерию Байеса относительно выигрышей будет равен …

Тогда средний выигрыш игрока по критерию Байеса относительно выигрышей будет равен …
Функция полезности потребителя имеет вид 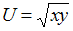 , а бюджетное ограничение
, а бюджетное ограничение 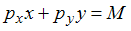 . Оптимальный набор благ потребителя:
. Оптимальный набор благ потребителя: 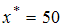 и
и  ,
,  . При уменьшении дохода на 1 единицу значение множителя Лагранжа
. При уменьшении дохода на 1 единицу значение множителя Лагранжа 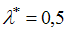 соответствует…
соответствует…
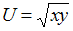 , а бюджетное ограничение
, а бюджетное ограничение 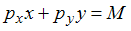 . Оптимальный набор благ потребителя:
. Оптимальный набор благ потребителя: 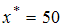 и
и  ,
,  . При уменьшении дохода на 1 единицу значение множителя Лагранжа
. При уменьшении дохода на 1 единицу значение множителя Лагранжа 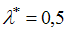 соответствует…
соответствует…Для определенного интеграла  справедливо неравенство …
справедливо неравенство …
 справедливо неравенство …
справедливо неравенство …Матрица рисков в игре с природой имеет вид:

Тогда средний риск игрока по критерию Байеса относительно рисков будет равен …

Тогда средний риск игрока по критерию Байеса относительно рисков будет равен …
Определенный интеграл  равен …
равен …
 равен …
равен …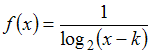 имеет вид
имеет вид 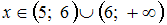 . Тогда значение
. Тогда значение 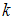 равно …
равно …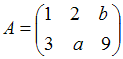 равен единице, если
равен единице, если 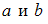 принимают значения …
принимают значения …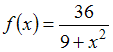 на отрезке
на отрезке 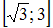 равно …
равно …