Математика – страница 174
Пусть 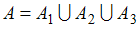 , причём для любых индексов
, причём для любых индексов 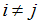
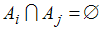 , т.е. множества
, т.е. множества 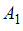 ,
, 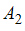 и
и 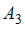 образуют разбиение множества
образуют разбиение множества 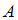 на подмножества.
на подмножества.
Известно, что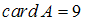 (
(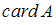 – число элементов множества
– число элементов множества 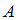 ),
), 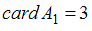 ,
, 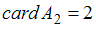 ,
, 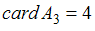 .
.
Тогда число вариантов разбиения множества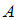 на подмножества указанным выше способом равно …
на подмножества указанным выше способом равно …
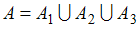 , причём для любых индексов
, причём для любых индексов 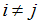
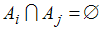 , т.е. множества
, т.е. множества 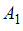 ,
, 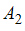 и
и 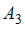 образуют разбиение множества
образуют разбиение множества 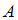 на подмножества.
на подмножества.Известно, что
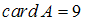 (
(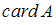 – число элементов множества
– число элементов множества 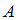 ),
), 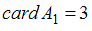 ,
, 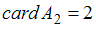 ,
, 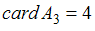 .
.Тогда число вариантов разбиения множества
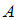 на подмножества указанным выше способом равно …
на подмножества указанным выше способом равно …Предел 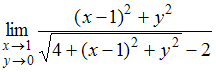 равен …
равен …
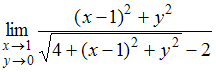 равен …
равен …Гармоническое колебание 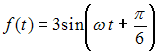 можно представить в виде …
можно представить в виде …
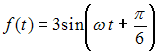 можно представить в виде …
можно представить в виде …5 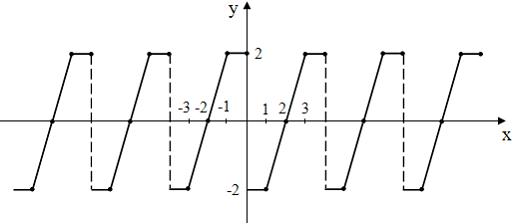
На рисунке изображен график функции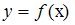
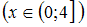 с ее периодическим продолжением. Периодическое продолжение
с ее периодическим продолжением. Периодическое продолжение 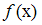 на числовую прямую является …
на числовую прямую является …

На рисунке изображен график функции
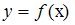
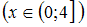 с ее периодическим продолжением. Периодическое продолжение
с ее периодическим продолжением. Периодическое продолжение 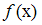 на числовую прямую является …
на числовую прямую является …Выборочное уравнение парной регрессии имеет вид 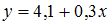 , а выборочные средние квадратические отклонения равны:
, а выборочные средние квадратические отклонения равны: 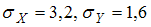 . Тогда выборочный коэффициент корреляции
. Тогда выборочный коэффициент корреляции 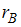 равен …
равен …
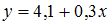 , а выборочные средние квадратические отклонения равны:
, а выборочные средние квадратические отклонения равны: 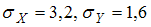 . Тогда выборочный коэффициент корреляции
. Тогда выборочный коэффициент корреляции 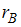 равен …
равен …Систему линейных уравнений 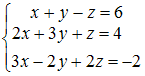 можно привести к виду …
можно привести к виду …
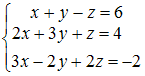 можно привести к виду …
можно привести к виду …Интеграл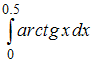 вычисляется при помощи разложения подынтегральной функции в степенной ряд. Тогда его значение с точностью 0,001 равно …
вычисляется при помощи разложения подынтегральной функции в степенной ряд. Тогда его значение с точностью 0,001 равно …
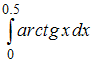 вычисляется при помощи разложения подынтегральной функции в степенной ряд. Тогда его значение с точностью 0,001 равно …
вычисляется при помощи разложения подынтегральной функции в степенной ряд. Тогда его значение с точностью 0,001 равно …Для функции 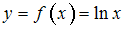 известны её значения в узлах
известны её значения в узлах 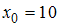 ,
, 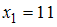 ,
, 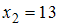 ,
, 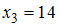 . Требуется вычислить значение этой функции в точке
. Требуется вычислить значение этой функции в точке 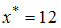 .
.
Для вычисления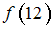 используется интерполяционный полином Лагранжа
используется интерполяционный полином Лагранжа 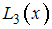 3-й степени. Погрешностями округлений пренебрегают.
3-й степени. Погрешностями округлений пренебрегают.
Тогда величина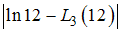 не превышает …
не превышает …
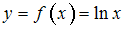 известны её значения в узлах
известны её значения в узлах 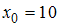 ,
, 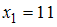 ,
, 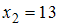 ,
, 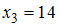 . Требуется вычислить значение этой функции в точке
. Требуется вычислить значение этой функции в точке 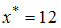 .
.Для вычисления
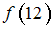 используется интерполяционный полином Лагранжа
используется интерполяционный полином Лагранжа 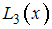 3-й степени. Погрешностями округлений пренебрегают.
3-й степени. Погрешностями округлений пренебрегают.Тогда величина
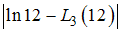 не превышает …
не превышает …В пространстве 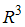 задано скалярное поле
задано скалярное поле 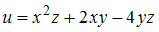 . Через точку
. Через точку 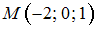 проходит поверхность уровня этого поля.
проходит поверхность уровня этого поля.
Тогда единичный вектор нормали к поверхности уровня в точке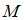 в направлении убывания поля равен …
в направлении убывания поля равен …
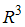 задано скалярное поле
задано скалярное поле 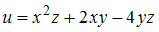 . Через точку
. Через точку 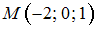 проходит поверхность уровня этого поля.
проходит поверхность уровня этого поля.Тогда единичный вектор нормали к поверхности уровня в точке
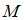 в направлении убывания поля равен …
в направлении убывания поля равен …Даны числовые множества 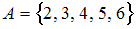 и
и 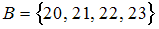 .
.
Между элементами этих множеств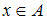 и
и 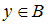 введено бинарное отношение
введено бинарное отношение 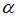 следующим образом:
следующим образом: 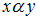 , если числа
, если числа 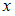 и
и 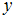 взаимно просты. Тогда указанное бинарное отношение можно описать матрицей …
взаимно просты. Тогда указанное бинарное отношение можно описать матрицей …
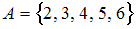 и
и 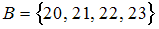 .
. Между элементами этих множеств
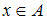 и
и 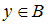 введено бинарное отношение
введено бинарное отношение 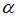 следующим образом:
следующим образом: 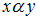 , если числа
, если числа 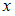 и
и 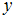 взаимно просты. Тогда указанное бинарное отношение можно описать матрицей …
взаимно просты. Тогда указанное бинарное отношение можно описать матрицей …Таблица
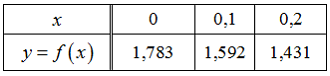
представляет значения функции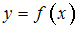 в некоторых точках.
в некоторых точках.
Используя формулы, основанные на интерполяционном полиноме Лагранжа, вычисляются, с тремя знаками после запятой, значения производной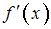 заданной функции в точках
заданной функции в точках 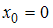 ,
, 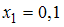 ,
, 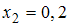 .
.
Тогда значения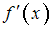 в указанных точках соответственно равны …
в указанных точках соответственно равны …

представляет значения функции
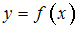 в некоторых точках.
в некоторых точках.Используя формулы, основанные на интерполяционном полиноме Лагранжа, вычисляются, с тремя знаками после запятой, значения производной
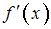 заданной функции в точках
заданной функции в точках 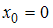 ,
, 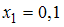 ,
, 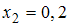 .
.Тогда значения
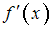 в указанных точках соответственно равны …
в указанных точках соответственно равны …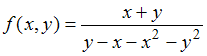 в точке
в точке 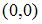 равен …
равен …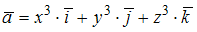 через поверхность куба
через поверхность куба 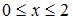 ,
, 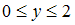 ,
, 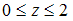 равен …
равен …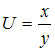 в точках
в точках 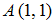 и
и 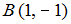 равен …
равен …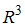 задано векторное поле
задано векторное поле 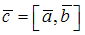 , где
, где 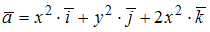 ,
, 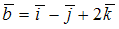 .
. 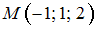 ротор этого поля имеет значение …
ротор этого поля имеет значение …