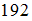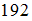Пусть 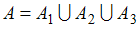 , причём для любых индексов
, причём для любых индексов 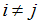
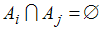 , т.е. множества
, т.е. множества 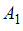 ,
, 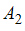 и
и 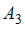 образуют разбиение множества
образуют разбиение множества 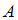 на подмножества.
на подмножества.
Известно, что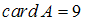 (
(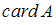 – число элементов множества
– число элементов множества 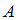 ),
), 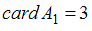 ,
, 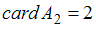 ,
, 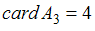 .
.
Тогда число вариантов разбиения множества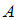 на подмножества указанным выше способом равно …
на подмножества указанным выше способом равно …
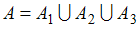 , причём для любых индексов
, причём для любых индексов 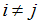
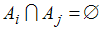 , т.е. множества
, т.е. множества 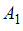 ,
, 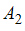 и
и 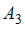 образуют разбиение множества
образуют разбиение множества 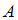 на подмножества.
на подмножества.Известно, что
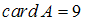 (
(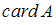 – число элементов множества
– число элементов множества 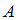 ),
), 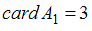 ,
, 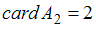 ,
, 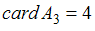 .
.Тогда число вариантов разбиения множества
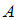 на подмножества указанным выше способом равно …
на подмножества указанным выше способом равно …• 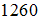
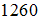
• 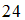
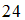
• 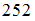
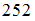
•