Линейная алгебра – страница 3
Линейное преобразование f в базисе 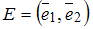 имеет матрицу
имеет матрицу 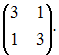 Тогда матрица этого оператора в базисе
Тогда матрица этого оператора в базисе 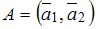 , где
, где 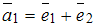 ;
; 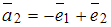 , имеет вид …
, имеет вид …
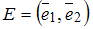 имеет матрицу
имеет матрицу 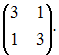 Тогда матрица этого оператора в базисе
Тогда матрица этого оператора в базисе 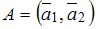 , где
, где 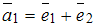 ;
; 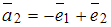 , имеет вид …
, имеет вид …Дана матрица 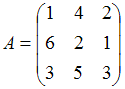 . Если
. Если 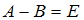 , где E – единичная матрица того же размера, что и матрица A, то матрица B равна …
, где E – единичная матрица того же размера, что и матрица A, то матрица B равна …
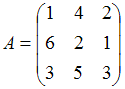 . Если
. Если 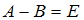 , где E – единичная матрица того же размера, что и матрица A, то матрица B равна …
, где E – единичная матрица того же размера, что и матрица A, то матрица B равна …Дано общее уравнение плоскости 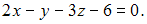 Тогда уравнение этой плоскости «в отрезках» имеет вид …
Тогда уравнение этой плоскости «в отрезках» имеет вид …
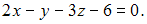 Тогда уравнение этой плоскости «в отрезках» имеет вид …
Тогда уравнение этой плоскости «в отрезках» имеет вид …Линейный оператор переводит векторы 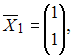
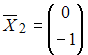 в векторы
в векторы 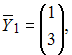
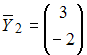 соответственно. Тогда матрица этого оператора имеет вид …
соответственно. Тогда матрица этого оператора имеет вид …
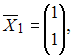
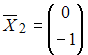 в векторы
в векторы 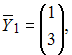
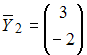 соответственно. Тогда матрица этого оператора имеет вид …
соответственно. Тогда матрица этого оператора имеет вид …Каноническое уравнение прямой, проходящей через начало координат перпендикулярно прямым 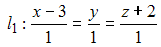 и
и 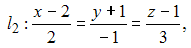 имеет вид …
имеет вид …
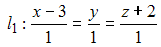 и
и 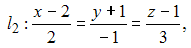 имеет вид …
имеет вид …Линейный оператор 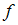 отображает базис
отображает базис 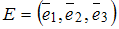 в векторы:
в векторы:
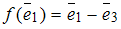 ;
; 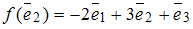 ;
; 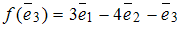 . Тогда матрица оператора
. Тогда матрица оператора 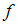 в этом базисе имеет вид …
в этом базисе имеет вид …
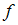 отображает базис
отображает базис 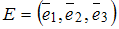 в векторы:
в векторы: 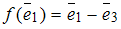 ;
; 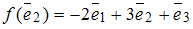 ;
; 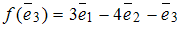 . Тогда матрица оператора
. Тогда матрица оператора 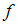 в этом базисе имеет вид …
в этом базисе имеет вид …Аксиомой линейного пространства 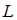 является …
является …
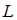 является …
является …Для элементов линейного пространства операции сложения и умножения на действительное число обладают свойством …
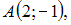
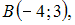
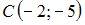 уравнение высоты, проведенной из вершины C, имеет вид …
уравнение высоты, проведенной из вершины C, имеет вид …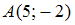 и
и 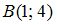 . Тогда координаты середины отрезка AB равны …
. Тогда координаты середины отрезка AB равны …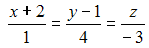 и плоскостью
и плоскостью 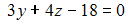 равно …
равно …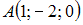 параллельно прямой
параллельно прямой 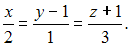
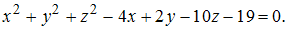
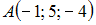 и
и 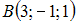 имеет вид …
имеет вид …