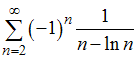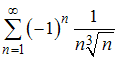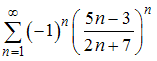Математика – страница 163
Методом Эйлера с шагом 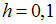 решается задача Коши для системы дифференциальных уравнений
решается задача Коши для системы дифференциальных уравнений

с начальными условиями ,
, 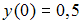 .
.
Тогда значения искомых функций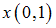 и
и 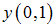 равны …
равны …
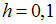 решается задача Коши для системы дифференциальных уравнений
решается задача Коши для системы дифференциальных уравнений 
с начальными условиями
 ,
, 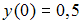 .
.Тогда значения искомых функций
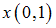 и
и 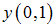 равны …
равны …Общее решение линейного однородного дифференциального уравнения второго порядка 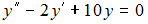 имеет вид …
имеет вид …
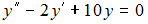 имеет вид …
имеет вид …Поле направлений дифференциального уравнения 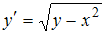 занимает заштрихованную область координатной плоскости …
занимает заштрихованную область координатной плоскости …
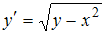 занимает заштрихованную область координатной плоскости …
занимает заштрихованную область координатной плоскости …Разложение в ряд Маклорена функции 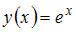 имеет вид:
имеет вид:  .
.
Тогда разложением в ряд по целым неотрицательным степеням переменной х функции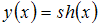 является …
является …
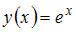 имеет вид:
имеет вид:  .
.
Тогда разложением в ряд по целым неотрицательным степеням переменной х функции
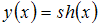 является …
является …Даны последовательности действительных чисел:
1)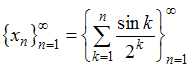 ,
,
2)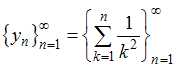 ,
,
которые исследуются с помощью критерия Коши.
Тогда истинным является утверждение, что …
1)
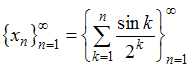 ,
,2)
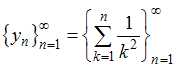 ,
,которые исследуются с помощью критерия Коши.
Тогда истинным является утверждение, что …
Сумма ряда  равна …
равна …
 равна …
равна …
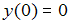 имеет вид …
имеет вид …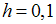 решается задача Коши
решается задача Коши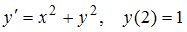 .
. искомой функции равно …
искомой функции равно …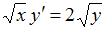 ,
,  имеет вид …
имеет вид …

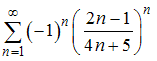

 , где
, где 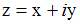 , имеет вид …
, имеет вид … решать задачу Коши
решать задачу Коши 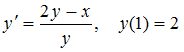 ,
, 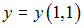 искомой функции будет равно …
искомой функции будет равно …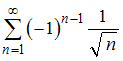 ;
;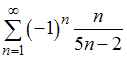 .
. фигуры, ограниченной параболами
фигуры, ограниченной параболами  и
и  , равен …
, равен …