Математика – страница 108
Пусть 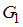 – группа всех положительных рациональных чисел относительно операции обычного умножения;
– группа всех положительных рациональных чисел относительно операции обычного умножения; 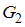 – группа всех действительных чисел относительно операции обычного сложения.
– группа всех действительных чисел относительно операции обычного сложения.
Тогда отображение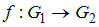 , определяемое соотношением
, определяемое соотношением 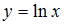 , где
, где 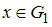 ,
, 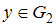 , …
, …
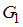 – группа всех положительных рациональных чисел относительно операции обычного умножения;
– группа всех положительных рациональных чисел относительно операции обычного умножения; 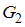 – группа всех действительных чисел относительно операции обычного сложения.
– группа всех действительных чисел относительно операции обычного сложения.Тогда отображение
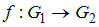 , определяемое соотношением
, определяемое соотношением 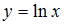 , где
, где 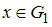 ,
, 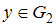 , …
, …Квадрат целого числа, меньшего пяти, умножили на само это число, увеличенное на четырнадцать. Тогда наибольшее значение такого произведения равно …
В топологическом пространстве 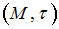 , где
, где 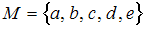 ,
,
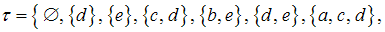
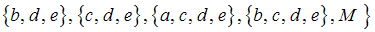
– совокупность всех открытых множеств этого пространства,
замыкание множества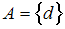 есть …
есть …
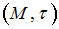 , где
, где 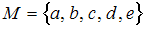 ,
, 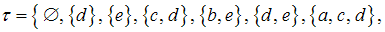
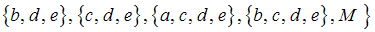
– совокупность всех открытых множеств этого пространства,
замыкание множества
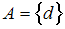 есть …
есть …Из указанных метрических пространств:
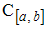 – множество всех непрерывных действительных функций, определенных на отрезке
– множество всех непрерывных действительных функций, определенных на отрезке 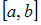 с расстоянием
с расстоянием 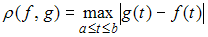 ;
;
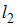 – пространство, точками которого служат всевозможные последовательности
– пространство, точками которого служат всевозможные последовательности 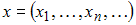 действительных чисел, удовлетворяющие условию
действительных чисел, удовлетворяющие условию 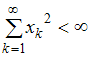 , а расстояние определяется формулой
, а расстояние определяется формулой 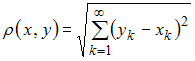 ;
;
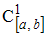 – множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке
– множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке 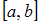 с расстоянием
с расстоянием 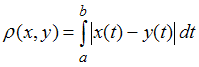 ;
;
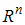 – множество упорядоченных групп из n действительных чисел
– множество упорядоченных групп из n действительных чисел 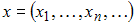 с расстоянием
с расстоянием 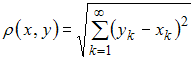 , –
, –
полным не является …
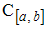 – множество всех непрерывных действительных функций, определенных на отрезке
– множество всех непрерывных действительных функций, определенных на отрезке 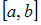 с расстоянием
с расстоянием 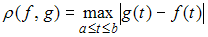 ;
;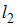 – пространство, точками которого служат всевозможные последовательности
– пространство, точками которого служат всевозможные последовательности 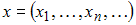 действительных чисел, удовлетворяющие условию
действительных чисел, удовлетворяющие условию 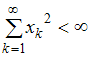 , а расстояние определяется формулой
, а расстояние определяется формулой 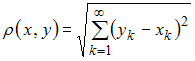 ;
;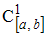 – множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке
– множество всех непрерывно дифференцируемых действительных функций, определенных на отрезке 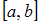 с расстоянием
с расстоянием 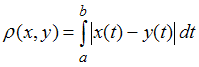 ;
;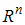 – множество упорядоченных групп из n действительных чисел
– множество упорядоченных групп из n действительных чисел 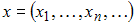 с расстоянием
с расстоянием 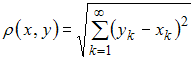 , –
, –полным не является …
Дано однопараметрическое семейство кривых на плоскости
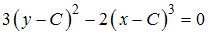 ,
,
где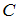 – параметр.
– параметр.
Тогда дискриминанта этого семейства кривых определяется уравнениями …
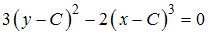 ,
,где
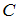 – параметр.
– параметр.Тогда дискриминанта этого семейства кривых определяется уравнениями …
Среди представленных множеств линейного пространства не образует…
Квадратичную форму от переменных 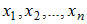 над полем
над полем 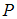 можно определить как ___________ с коэффициентами из поля
можно определить как ___________ с коэффициентами из поля 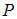 .
.
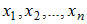 над полем
над полем 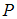 можно определить как ___________ с коэффициентами из поля
можно определить как ___________ с коэффициентами из поля 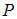 .
.В химическом продукте могут оказаться примеси четырех видов: 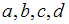 . Тогда существует ___ варианта(-ов) содержания в нем примесей только двух видов.
. Тогда существует ___ варианта(-ов) содержания в нем примесей только двух видов.
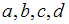 . Тогда существует ___ варианта(-ов) содержания в нем примесей только двух видов.
. Тогда существует ___ варианта(-ов) содержания в нем примесей только двух видов.Корень уравнения 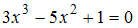 отделен на отрезке …
отделен на отрезке …
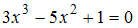 отделен на отрезке …
отделен на отрезке …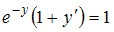 при
при 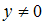 можно представить как …
можно представить как …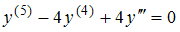 имеет вид…
имеет вид…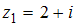 ,
, 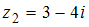 и
и 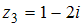 , то выражение
, то выражение 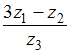 равно …
равно …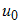 и
и 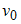 являются решением системы линейных уравнений
являются решением системы линейных уравнений 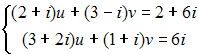 , то
, то 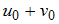 равно …
равно …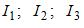 уравнения кривой второго порядка
уравнения кривой второго порядка 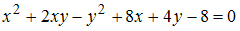 равны …
равны …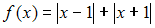 в точке
в точке 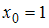 равна …
равна …