Дан доверительный интервал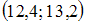 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
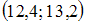для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна … • 12,7
Совершена арифметическая ошибка при вычислении точечной оценки.
• 12,8
• 0,4
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки.
• 13,0
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки.