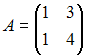 , то обратная к ней матрица
, то обратная к ней матрица 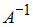 равна …
равна … 
Для нахождения обратной матрицы методом элементарных преобразований записывают расширенную матрицу, содержащую в правой части единичную матрицу размерности, одинаковой с исходной. С использованием элементарных преобразований, расширенная матрица приводится к виду, при котором исходная матрица (левая часть) превращена в единичную. Тогда правая часть расширенной матрицы содержит матрицу обратную данной.


Для нахождения обратной матрицы методом элементарных преобразований записывают расширенную матрицу, содержащую в правой части единичную матрицу размерности, одинаковой с исходной. С использованием элементарных преобразований, расширенная матрица приводится к виду, при котором исходная матрица (левая часть) превращена в единичную. Тогда правая часть расширенной матрицы содержит матрицу обратную данной.
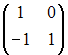
Для нахождения обратной матрицы методом элементарных преобразований записывают расширенную матрицу, содержащую в правой части единичную матрицу размерности, одинаковой с исходной. С использованием элементарных преобразований, расширенная матрица приводится к виду, при котором исходная матрица (левая часть) превращена в единичную. Тогда правая часть расширенной матрицы содержит матрицу обратную данной.