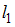На плоскости заданы множество точек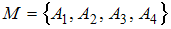 
, причём точки заданы своими координатами 
, 
, 
, 
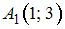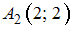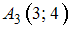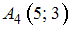, и две прямые 
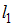и 
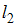своими уравнениям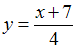и 
и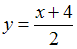 
соответственно. Мерой близости множества точек и прямой будем считать сумму квадратов соответствующих расстояний (как в методе наименьших квадратов).
Тогда справедливо утверждение:
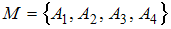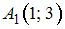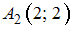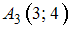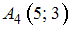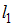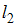, причём точки заданы своими координатами , , , , и две прямые и своими уравнениям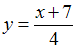и и 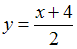соответственно. Мерой близости множества точек и прямой будем считать сумму квадратов соответствующих расстояний (как в методе наименьших квадратов).Тогда справедливо утверждение:
• прямые лини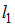и 
и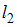 
одинаково близки к множеству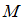 
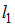и 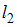одинаково близки к множеству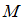 • меры близости разных прямых линий к одному и тому же множеству сравнивать нельзя
• прямая линия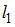 
расположена ближе к множеству 
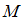, нежели прямая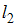 
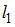расположена ближе к множеству 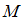, нежели прямая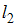 • прямая линия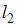 
расположена ближе к множеству 
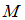, нежели прямая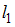 
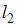расположена ближе к множеству 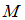, нежели прямая