Математика и информатика – страница 50
Для оценки с некоторой надежностью  математического ожидания
математического ожидания 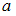 нормально распределенного признака
нормально распределенного признака 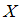 по выборочной средней
по выборочной средней 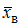 при среднем квадратичном отклонении
при среднем квадратичном отклонении 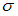 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 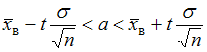 , где
, где 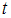 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 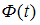 , при котором
, при котором  ,
, 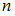 – объем выборки.
– объем выборки.
Установите соответствие между доверительными интервалами и выборочными средними, по которым они получены.
1.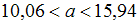
2.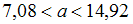
 математического ожидания
математического ожидания 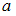 нормально распределенного признака
нормально распределенного признака 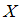 по выборочной средней
по выборочной средней 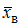 при среднем квадратичном отклонении
при среднем квадратичном отклонении 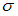 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 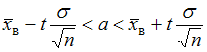 , где
, где 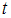 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 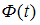 , при котором
, при котором  ,
, 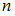 – объем выборки.
– объем выборки.Установите соответствие между доверительными интервалами и выборочными средними, по которым они получены.
1.
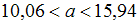
2.
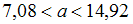
Для отбора документов, в которых отсутствует ключевое слово, в поисковой машине Google в поле запроса необходимо …
Для оценки с надежностью 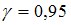 математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака 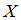 по выборочной средней
по выборочной средней  при среднем квадратичном отклонении
при среднем квадратичном отклонении 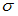 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал  , где
, где 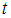 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  , при котором
, при котором  ,
, 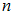 – объем выборки.
– объем выборки.
Установите соответствие между доверительными интервалами и соответствующими значениями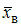 :
:
1)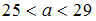 ,
,
2)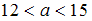 .
.
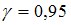 математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака 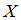 по выборочной средней
по выборочной средней  при среднем квадратичном отклонении
при среднем квадратичном отклонении 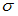 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал  , где
, где 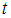 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  , при котором
, при котором  ,
, 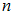 – объем выборки.
– объем выборки.Установите соответствие между доверительными интервалами и соответствующими значениями
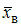 :
:1)
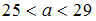 ,
,2)
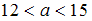 .
.Для поиска веб-страниц, содержащих информацию о крупных животных Африки, кроме БЕГЕМОТА и ГИППОПОТАМА, в поле запроса в поисковой машине Google необходимо ввести …
Число 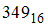 , записанное в восьмеричной системе счисления, имеет вид …
, записанное в восьмеричной системе счисления, имеет вид …
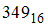 , записанное в восьмеричной системе счисления, имеет вид …
, записанное в восьмеричной системе счисления, имеет вид …Количество двоичных разрядов в числе 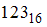 , записанном в двоичной системе счисления, равно …
, записанном в двоичной системе счисления, равно …
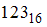 , записанном в двоичной системе счисления, равно …
, записанном в двоичной системе счисления, равно …Для оценки с надежностью 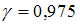 математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака 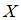 по выборочной средней
по выборочной средней 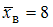 при среднем квадратичном отклонении
при среднем квадратичном отклонении  генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 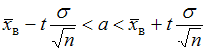 , где
, где 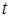 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 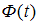 , при котором
, при котором 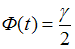 ,
, 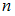 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для 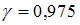 равно
равно 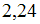 . Объем выборки равен
. Объем выборки равен 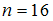 .
.
Установите соответствие между средними квадратическими отклонениями и соответствующим доверительными интервалами.
и соответствующим доверительными интервалами.
1.
2.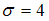
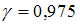 математического ожидания
математического ожидания  нормально распределенного признака
нормально распределенного признака 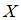 по выборочной средней
по выборочной средней 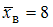 при среднем квадратичном отклонении
при среднем квадратичном отклонении  генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 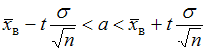 , где
, где 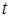 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 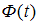 , при котором
, при котором 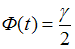 ,
, 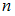 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для 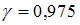 равно
равно 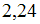 . Объем выборки равен
. Объем выборки равен 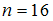 .
.Установите соответствие между средними квадратическими отклонениями
 и соответствующим доверительными интервалами.
и соответствующим доверительными интервалами.1.

2.
Имеются два ящика с шарами. В первом ящике содержится 15 белых и 5 черных шаров, во втором – 18 белых и 12 черных шаров.
Установите соответствие между следующими вероятностями и их значениями.
1. Вероятность того, что наудачу взятый шар из первого ящика белый.
2. Вероятность того, что наудачу взятый шар из второго ящика белый.
3. Вероятность того, что наудачу взятый шар из наудачу взятого ящика белый.
Установите соответствие между следующими вероятностями и их значениями.
1. Вероятность того, что наудачу взятый шар из первого ящика белый.
2. Вероятность того, что наудачу взятый шар из второго ящика белый.
3. Вероятность того, что наудачу взятый шар из наудачу взятого ящика белый.
Даны высказывания 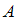 – «
– «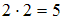 » и
» и 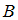 – «
– «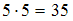 ». Тогда высказывание «Если
». Тогда высказывание «Если 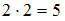 , то
, то 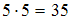 » является ___________ этих высказываний.
» является ___________ этих высказываний.
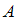 – «
– «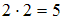 » и
» и 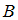 – «
– «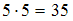 ». Тогда высказывание «Если
». Тогда высказывание «Если 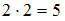 , то
, то 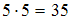 » является ___________ этих высказываний.
» является ___________ этих высказываний.Даны числовые множества:
 – множество натуральных чисел,
– множество натуральных чисел,
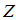 – множество целых чисел,
– множество целых чисел,
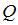 – множество рациональных чисел,
– множество рациональных чисел,
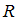 – множество действительных чисел.
– множество действительных чисел.
 .
.
Известно, что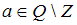 . Тогда справедливо утверждение, что …
. Тогда справедливо утверждение, что …
 – множество натуральных чисел,
– множество натуральных чисел,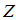 – множество целых чисел,
– множество целых чисел,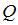 – множество рациональных чисел,
– множество рациональных чисел,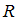 – множество действительных чисел.
– множество действительных чисел. .
.Известно, что
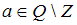 . Тогда справедливо утверждение, что …
. Тогда справедливо утверждение, что …Два преподавателя проверяют работы письменного экзамена по математике. Вероятность того, что работа попадет к первому преподавателю (событие  ), равна 0,55, ко второму (событие
), равна 0,55, ко второму (событие 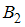 ) – 0,45. Вероятность того, что первый преподаватель забудет заверить проверенную работу, равна 0,04, а второй – 0,02. Для расчета вероятности того, что выбранная наудачу работа не была заверена (событие
) – 0,45. Вероятность того, что первый преподаватель забудет заверить проверенную работу, равна 0,04, а второй – 0,02. Для расчета вероятности того, что выбранная наудачу работа не была заверена (событие 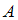 ), используется формула полной вероятности
), используется формула полной вероятности 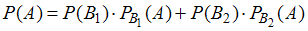 . Установите соответствие между обозначениями вероятностей и их числовыми значениями:
. Установите соответствие между обозначениями вероятностей и их числовыми значениями:
1)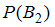 ,
,
2)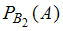 ,
,
3)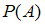 .
.
 ), равна 0,55, ко второму (событие
), равна 0,55, ко второму (событие 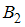 ) – 0,45. Вероятность того, что первый преподаватель забудет заверить проверенную работу, равна 0,04, а второй – 0,02. Для расчета вероятности того, что выбранная наудачу работа не была заверена (событие
) – 0,45. Вероятность того, что первый преподаватель забудет заверить проверенную работу, равна 0,04, а второй – 0,02. Для расчета вероятности того, что выбранная наудачу работа не была заверена (событие 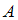 ), используется формула полной вероятности
), используется формула полной вероятности 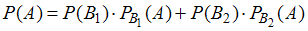 . Установите соответствие между обозначениями вероятностей и их числовыми значениями:
. Установите соответствие между обозначениями вероятностей и их числовыми значениями:1)
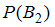 ,
,2)
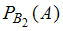 ,
,3)
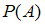 .
.Два контролера проверяют детали на стандартность. Вероятность того, что деталь попадет к первому контролеру, равна 0,4, ко второму – 0,6. Вероятность того, что первый контролер признает деталь стандартной, равна 0,8, второй –  . Деталь при проверке была признана стандартной.
. Деталь при проверке была признана стандартной.
Установите соответствие между значениями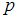 и вероятностью того, что деталь признал стандартной второй контролер.
и вероятностью того, что деталь признал стандартной второй контролер.
1.
2.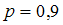
 . Деталь при проверке была признана стандартной.
. Деталь при проверке была признана стандартной. Установите соответствие между значениями
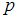 и вероятностью того, что деталь признал стандартной второй контролер.
и вероятностью того, что деталь признал стандартной второй контролер. 1.

2.
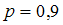
Даны множества:
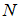 – множество натуральных чисел,
– множество натуральных чисел,
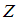 – множество целых чисел.
– множество целых чисел.
Тогда истинно следующее высказывание:
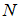 – множество натуральных чисел,
– множество натуральных чисел,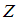 – множество целых чисел.
– множество целых чисел.Тогда истинно следующее высказывание:
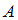 и
и 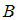 соответствует формула …
соответствует формула …